|

|
"If you want to build a ship, don't herd people together to collect wood and don't assign them tasks and work, rather teach them to long for the endless immensity of the sea." [Translation of French][15]
MathPath is a national summer program for
students of middle school age (11 to 14 years) showing high promise in mathematics.
"MathPath is unique; there are no other national summer programs exclusivley in math for this middle school group. There are science programs for them, and engineering programs, and more general programs like the Johns Hopkins CTY program, but nothing else for the summer which is exclusively math and gets kids into the culture of the profession as well as challenging them mathematically at this age. There are, to be sure, math programs for *high school* kids (including MathPath's sister program, MathCamp), but so far, a middle school program is unique. The idea was suggested by John Conway."
-- Prof. Stephen Maurer, Swarthmore College (Excerpt from a 2004 letter to Professors Philip Davis and Thomas Banchoff)
The outside square has double the area of the inner one - Socrates is said to have made a boy realize this. [14]
Why MathPath Exists?
In the epic novel [17], Tom Joad is unfazed when their ancient car breaks down on the highway. He confidently goes about fixing it. The fellow traveller and ex-preacher, Jim Casy, asks Tom: "Funny how you fellas can fix a car." Tom replies: "GOT TO GROW INTO IT WHEN YOU'RE A LITTLE KID."
Starting at an early age is even more relevant in fields like sports, music, and math where attainment level spans a wide spectrum. So, to become good at doing math, a person needs to get in to math early! This is what parents and teachers of the gifted try to help children to do. But then, why MathPath?
MathPath exists in answer to this one question: What is the early mathematics education appropriate for students who love mathematics?
MathPath would have no reason to exist if all middle schools provided appropriate experiences for these students. However, such instruction can not be practical in a school unless either many students there love mathematics or the school has huge resources to spread out also to the few with the mathematics inclination. So MathPath exists!
A mathematician can be likened to a concert hall. The greatness of a concert hall is determined by its initial design. The greatness of a mathematician is determined by the quality of her/his mathematical research work, but the greatness is a consequence of the individual's genetic make up, environment and early education.
It has been the practice of parents of students attending grades 6-8 and showing high promise in mathematics to send them to summer programs attended mainly by high school students. The younger students in the age range of 11-14 were thus thrown in with highschoolers in the age range of 15-19. Since a typical high school program took in just a few students 11 to 14 years of age, those students were deprived of the opportunity of being with others in their age range. While young students may want to be with much older kids and while parents want their young one to be accelerated quickly to the level of the high school students, the need to be with others closer in age is lost. MathPath takes in students in the age range of 11-14 and provides an enrichment program appropriate for the exceptionally gifted who love math. Thus the student gets a matching program that avoids the disadvantage of having the student sit in class in which everyone else is so much older.
What are the Appropriate Special Experiences for the Future Mathematician of Middleschool Age?
Exceptionally gifted students who love mathematics absorb mathematical ideas at a faster rate. So "some" acceleration - high school courses for the middle schooler - is needed and these are easily available for the student in either the school itself or the school district. Acceleration is the easy path but not the most desireable. It is more desireable to go for the "
breadth of mathematics, by allowing quicker students to work through the material
in greater depth and to take excursions into related topics, before racing ahead of
their age group."[19]
"The structure of mathematics is not like a tree, but more like a scaffolding, with many interconnected supports."[19] Highly gifted students will be better served by opportunities to learn the connected subjects so they can begin to see the interconnections. What this means is that a broad mathematics education - enrichment - is preferable to too much acceleration. "The shape of the mathematics education of a typical student is tall and spindly. It reaches a certain height above which its base can support no more growth, and there it halts or fails." [19]
"By the time
they are 25 or 30, they are judged not by precociousness but on the quality of work." [19]
"To get a degree at a young age, to be a record-breaker, means nothing. I had a pyramid model of knowledge, that is, a very broad base and then the pyramid can go higher. If you just very quickly move up like a column, then you're more likely to wobble at the top and then collapse'' -- Dr. William Tao, father of Terrence Tao (Fields Medallist), on the early education of his son [4]
In such a broad education are strands that are not available in schools. And in the university curriculum, with the crowded core courses, the student does not have the time. So MathPath offers them - Proof, Writing in mathematics, Hyperbolic Geometry, Analytic Geometry, and the history of mathematics, to name a few areas.
Learning experiences that are not appropriate for the exceptionally and profoundly gifted include the following: rote learning, drilling, trivial arithmetical computations, over-reliance on calculators and computers, and being fed concepts without showing how they sit in the context of the general subject area. Here is an example of ignoring context. In the geometry strand in middle school and high school, students are given a list of Triangle Similarity theorems - AA, SAS, and SSS. Students memorize and use them. However, if students are shown how these sit in relation to triangle congruence theorems, why there are only three similarity theorems for triangles, and why none of these would work for quadrilaterals, they would get a better appreciation of the similarity concept, angle congruence, and the proportionality of corresponding sides for similar triangles.
It seems teaching in the sciences - for instances, Physics - does not have these ills to the same extent. Teaching Physics is teaching concepts - concepts in context. For instance, teaching the Archimedes Principle of Buoyancy is in the context of fluid pressure which is in the context of the equilibrium of forces. The context is forced on the teacher in the natural sciences, for the context is needed to explain the concept. So, in the natural sciences, context is not optional. But it is optional in improper mathematics instruction.
How the MathPath Summer Program is Different
The nature of the program is best explained by an example of its instructional approach. Consider the quadratic equation ax2 + bx + c = 0. The mathematically precocious in grade 6 may already know why the "roots" of the equation are given by
x= (- b ± √(b2-4ac))/2a by completing the left side of the quadratic equation into the perfect square (ax + b/2)2, which then must equal (b/2)2 - ac. Indeed, this is a beautiful and revealing piece of algebra. And this is where the schools and universities usually end the discussion. However, a complete mathematical analysis seeks more! What the solution says is that the two values found satisfy the given equation. But are there more values? No! But why? And is it possible for another quadratic equation to have these same roots? Yes, there are infinitely many quadratic equations with the same roots! When we try to prove these, we understand - "stand under" - the problem!
This is the fashion in which a mathematics problem is settled by a mathematician - in fact, a mathematician may not stop here; she/he may look at the "Inverse Problem", that is, starting with given roots, looking for all equations that have these roots. The inverse problem is usually more powerful and interesting, just us the inverse problem of the Pythagorean Theorem, which happens to be the converse of the theorem, which is so much more useful and whose standard proof[8] illustrates a proof-method for converses, yet is seldom taught in school. Unfortunately, in the setting of a general class in school, most students will not be able to appreciate the continued pursuit of a problem even if the teacher is knowledgeable enough. Finding the formula for the roots of a general quadratic equation in one variable is just problem-solving; settling the question by also showing the uniqueness of the roots as well as the class of quadratic equations that have the same roots is mathematics. The latter means "under standing." Now compare this to the standard approach in most classes where students are given the formula and asked to find the values of the roots. That is not mathematics but the application of mathematics to compute.
The proper education of the potential future mathematician entails more. In introducing a concept, the instructor must begin at the beginning and show the students how the concept evolved. This helps in fundamental understanding just as etymology does for a word. Imagine the routine start of a Group Theory course in university at the early part of the 21st century. The instructor would begin by writing out the boring axioms. Imagine, instead, if he/she recounted the story of Cayley[3] in the 19th century looking at the equation xn = 1 and realizing that the structure of the solution was the manifestation of a form - Group - that showed itself at many locations in the mathematics of that time. The discovery of a concept or theory is a story; telling the story is like bringing the discoverer - the greatest teaching assistant - into the classroom to introduce the subject. Students will stop doodling, and the axioms will enter the senses. These stories of mathematics emulate the dynamic of research mathematics and the construction of knowledge out of the activity of problem-solving. That is, they will show the struggles the human mind went through to arrive at the present form of the concept; they will show the creative process - not just the finished product -, for the mathematician similarly struggles with the problem until the answers slowly blossom in her/his mind. Neils Henrik Abel observed [1]: "It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils."
But Mr. Abel, studying the masters is difficult. There are few, if any, books in math like the historic fiction in literature. The story of a mathematical discovery is often not recorded by the discoverer. Someone has to piece it together. But that is very very difficult. Yes, the counterpart of historic fiction in math is difficult to create. Our recourse is the old professor who has the holistic view and can let us imagine the gropings by which the discovery occurred. We believe that a class for the future mathematician should be like Socrates enabling the boy realize - make real what could be knowledge that is already in the vast subconscious of the boy. For this to happen, we need three elements: Socrates, the boy, and an eagerness on the part of both to externalize what is already latent in the boy. Do we have the boys and girls? We do! The students at MathPath constitute a select group screened using a Qualifying Test that is unlike the time-limited national math contests. The Test is a sieve that produces students who love math and are smart and tenacious. These are students attending mostly grades 6-8 at the time of application. Many of them are taking high school courses. Do we have Socrates? NO! However, the teaching at MathPath is led by professors, picked from universities all over the nation, who are experts in teaching mathematically gifted middle school students in a way that often emulates Socrates. "Doing even elementary mathematics right involves substantial mathematical judgement and understanding, as well as an ability to listen to students and adapt instruction to their needs."[9] "In the mathematics, the higher one advances, the more widely does the horizon open around him."[7] Famous, older professors in general possess a holistic view and have the perspective of how a concept or object sits in relation to others, and thus they are able to impart an awareness of the common characteristic that is a mark of the general area relevant to the matter at hand. The great mathematician, A. Grothendieck, echoes this. [English translation] "If there is one thing in mathematics that fascinates me more than anything else (and doubtless always has), it is neither "number" nor "size", but always form. And among the thousand-and-one faces whereby form chooses to reveal itself to us, the one that fascinates me more than any other and continues to fascinate me is the structure hidden in mathematical things."[9]
But how is it possible in a general class to emulate Socrates? How could individual attention be paid? The answer lies in noting the higher talent level as well as the greater talent homogeneity at a summer program such as MathPath.
"The authority of those who profess to teach is very often an impediment to those who desire to learn."[5] "Socrates and, Arcesilaus, first made their scholars speak, and then they spoke to them."[13] In arriving at a mathematics proof of a theorem, the instructor at MathPath often shifts into the Socratic Method. In sum, the end of instruction here is to enable the student to see for himself or herself, with instructor as the aide - not the spoon.
The Moore Method [6] is in a sense a modified Socratic Method adapted to a class. That is, whereas, in the Socratic Method, questions asked by the teacher bring out the knowledge latent in the student, in the Moore Method, the questions are asked by the student to himself/herself. This empowers the student towards discovery learning.
The proper education of the exceptionally gifted young student who loves mathematics entails even more. To travel the mathematics path, they must not only know what constitutes proof, but also how to write mathematics properly and acquire the habit of asking the right questions. The path of mathematics advances from answers to questions.
The Academic Needs of the very gifted
The easy-looking solution for developing to the maximum the talents of gifted students is to enroll them in problem-solving activities. These are easily organized or available in outstanding schools or large school districts or local universities.
But problem-solving is only one aspect - an important aspect - of the early enhanced education of the potential future mathematician.
The highly gifted need broader and deeper challenges matching their gift.
This is achieved at MathPath through the several strands of interactive courses in
mathematics that the students will be immersed in so that they emerge from the program with a broader
and deeper understanding after having experienced mathematics,
particularly through "seeing" some of its historical development. Summer programs for the gifted are usually either intense problem-solving workshops or a single course in a mathematical subject. MathPath
is a multi-course, comprehensive summer program designed for the overall mathematical development of the future mathematician.
The great 20th century English Mathematician G.H.Hardy lamented[10] when his mathematical powers were waning in his sixties:
"Mathematics is a young man's - read 'person's' - game." It is true that most major mathematical
discoveries made were by people before they were forty. Thus in mathematics, as in music, an early professional
education is called for. Sir Michael Atiyah, the noted mathematician and Fields Medallist,
said [2] in "How Research is Carried Out": The very difficult mathematics of our predecessors ...
distilled out in such a way that we can teach it to mathematicians
at a very early age, and it is the only way in which we can compress
all our mathematical experience in to a form which it is possible
for our successors to absorb and continue.
What problem-solving activities are appropriate for the highly gifted?
MathPath is also a venue for high-ability students interested in improving their problem solving ability. "The need to be
challenged is central to high-ability students. They must be given
problems whose solution they cannot readily see. The hints and
stepping stones to a solution must be spread out widely and doled
out frugally. They must be free to think in many directions,
including those not pursued by the teacher."[16] Some of the most experienced problem-solving faculty and, under their supervision, undergraduate students who had nationally or internationally excelled in problem-solving, work with students at MathPath.
Problem-solving for the future mathematician should consist not only in contest training and heuristics.
"Related to precociousness is the popular tendency to think of mathematics as a
race or as an athletic competition. There are .... the state, national and international competitions. These competitions
are fun, interesting, and educationally effective for the people who are successful
in them. But they also have a downside. The competitions reinforce the notion
that either you "have good math genes", or you do not. They put an emphasis on
being quick, at the expense of being deep and thoughtful. They emphasize questions
which are puzzles with some hidden trick, rather than more realistic problems
where a systematic and persistent approach is important. This discourages many people who are not as quick or as practiced, but might be
good at working through problems when they have the time to think through them.
Some of the best performers on the contests do become good mathematicians, but
there are also many top mathematicians who were not so good on contest math.
Quickness is helpful in mathematics, but it is only one of the qualities which is
helpful. For people who do not become mathematicians, the skills of contest math
are probably even less relevant.
These contests are a bit like spelling bees. There is some connection between
good spelling and good writing, but the winner of the state spelling bee does not
necessarily have the talent to become a good writer, and some fine writers are not
good spellers. If there was a popular confusion between good spelling and good
writing, many potential writers would be unnecessarily discouraged." - [19] William Thurston (Fields Medallist)
The problems appropriate for the highly gifted are what are called "dangling" problems. These are problems that are easily stated, "easily understood, have intuitive appeal, and are wide open to student initiative in experimenting, formulating questions, conjecturing, and proving."[12] Dangling such a question before even moderately gifted students usually leads to general participation in discussion, individual efforts, or even research projects. Dangling problems provide students with a "participatory glimpse of mathematics in the making." That is, the students will think a lot of interesting questions that will extend the problem and try to answer them. The various questions one can ask about extending the problem are the dangles.
A dangling problem is not necessarily a question. Its dangles are the questions. Kenneth O. May [12] gives the Galileo Sequence as an example of a dangling problem:
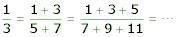
At this time - the year 2003 A.D. - the world has hundreds of books on problems and problem-solving. Let a book of dangling problems be written.
The need of the highly gifted to meet and work with peers
The professional mathematician is in regular interaction with peers. This is necessary in order to learn about new discoveries, new approaches to unsolved problems, and new ideas, or to engage in collaborative research. In the early years of the future mathematician this future interaction tendency exhibits itself as a craving to spend time with peers.
MathPath is a summer gathering place for middle school students of high mathematical ability. Their greatest social need is
to meet peers. "The most valuable resource
that high-ability students can be given is access to each other's
minds."[16]
The inadequacy of regular school instruction for the highly gifted
A 1993 report by the U.S. Department of Education found that
only 2 cents out of every $100 spent on precollegiate education in 1990
went to gifted programs. Education Secretary Richard W. Riley described
the situation as a "quiet crisis" in which the needs of the
nation's ablest students are seldom met.
Six decades after influential psychologist Lewis Terman [18] warned against
indifference to the special needs of budding geniuses, the general attitude
hasn't changed: Why invest in the high-IQ child who'll learn fine wherever
he/she is? It's the struggling masses who need the help.
"The argument is, if we just have limited resources, why do we help
the kids who don't need help? But that assumes they don't need help."
[19]
"They need education that is challenging"[20] but don't often get
it. "These children are miserable in school when they
are forced to work way below their level." It is a demonstrated fact that the highly gifted are more in need
of specialized education than the moderately gifted.
Even the moderately gifted student in a regular class is under-serviced,
or at least not adequately challenged.
The website figurethis.org funded by the
NSF and the US Dept of Education has this to say in 2003 A.D.: "The world's most
reliable series of international comparative studies of educational
achievement, The Third International Mathematics and Science Study (TIMSS) shows that the mathematics curriculum in U.S. schools is
unfocused, repetitive and not very demanding. In non-algebra
courses, the curriculum is excessively focused on arithmetic. In
algebra courses, students spend too much time on low-level knowledge
and not enough time on complex problem-solving. The TIMSS study
videotaped instruction in 8th grade classrooms in the U.S., Germany
and Japan. The videotapes show that teaching in the U.S. emphasizes
low-level rather than high-level thinking. The teaching uses tasks
that encourage memorization and recall, rather than reasoning and
problem-solving. U.S. teaching also tends to state ideas rather than
develop them."
Mathematics performance of students improves if the instruction
is based on rigorous standards. Such standards as the Principles and Standards for School Mathematics (PSSM) developed by
the National Council of Teachers of Mathematics can address
this[11]. In PSSM and other documents to come we suggest that their recommendation of a topic in a mathematics course in school be determined not for its use in other areas of mathematics or real-world applications, rather for its role in deepening the understanding of the foundation - manipulation of symbols ( tell students at least what Viete did for mathematics, if not what Frege did for logic, in introducing symbols), proof, writing, and using topics of just elementary mathematics as aids to illustrate. School geometry will then come alive and exciting. Proof will then vie with computer games in capturing the interest and imagination of the youngsters.
Thus we would suggest that the easy solution to enrol a gifted student in an AP Course or an e-course such as the one offered by EPGY is at best a partial solution. The very gifted, and even others, should be given the chisel and the stone, not the finished statues to behold as would pollution-producing tourists.
We are also advocating that this is the least that gifted extra-school and summer programs should achieve, for their job is easier in that they are preaching to the converted. Meanwhile ways to improve America's school instruction must be sought.
Instruction appropriate for the highly gifted would still be not met. The talented few who could go deeper and further can not be
adequately challenged by the content and pace in a regular class of a spectrum of abilities. Nor will it be easy to set apart time
in the teacher's already busy schedule to provide special enrichment
sessions for the very few gifted students in the large class or school. Allowing enough released time for a teacher to act as "math team coach" to work with these students is, therefore, at least a partial solution. But the highly gifted need more!
Other Issues
The possessor of a gift pays in future a price commensurate with the extent of the gift, and mathematical gift is no exception to this. All we can, and what we can, do is ease their beginning journey by giving them the right environment - supportive not-over-pushy parents, at least one teacher - in large schools - provided with the incentives to mentor the very gifted, gifted peers found in special in-school or extra-school Instruction programs similar to the Math Circles, online instruction and information opportunities as in the Math Forum and the Art of Problem Solving websites, and appropriate summer opportunities according to the level of gift.
As of this writing in 2001, only 9% of all mathematicians are women. Research has shown
that a higher proportion of girls than boys lose interest in
mathematics during their middle school years. MathPath strives to
also recruit girls with the highest talent and give them instruction and
peers. This helps to reduce the attrition of girls possessing the
high talent.
The reward for the mathematicians who run MathPath is not only in the satisfaction of mentoring the future ones of their kind, but also in rescuing, through talent discovery and development, many a future mathematician from oblivion.
REFERENCES
[1] Abel, Niels Henrik, Memoirs de Mathematique, Oslo University Library - Confirming admiration of the work of Simon Laplace, in a note, dated 6 August 1826, scribbled in the margin on page 79 of volume 2 of Abel's "Paris Notebook" diary
[2] Atiyah, Michael, Collected Works, Vol. I, Oxford University Press, 1988
[3] Cayley, Arthur, On the Theory of Groups, as Depending on the Symbolic Equation qn = 1, The Collected Mathematical Papers of Arthur Cayley, vol. 1, 423--424; vol. 2, 123--132, Cambridge University Press, Cambridge, 1889
[4] Chang, Kenneth, Journey to the Distant Fields of Prime, New York Times, March 13, 2007
[5] Cicero, Marcus Tullius, De Natura Deorum, Harvard University Press, 1933
[6] Cohen, D.W., A Modified Moore Method for Teaching Undergraduate Mathematics, The American Mathematical Monthly, 89 (1982) 473Ð474; 487Ð490
[7] De Morgan, Augustus, Introductory lecture delivered at the opening of the mathematics classes in the University of London, November 5, 1828
[8] Heath, Thomas L., Proposition I.48 in Euclid - The Thirteen Books of the Elements, Vol. I, Dover Publications, 1956
[9] Grothendieck, Alexandre, Récoltes et semailles: Réflexions et témoignages sur un passé de mathématicien. Université des Sciences et Techniques du Languedoc, Montpellier, et Centre National de la Recherche Scientifique, 1986. The English translation quoted is taken from
Jackson, Allen, Comme Appelé du Néant - As If Summoned from the Void: The Life of Alexandre Grothendieck, Notices of the AMS, October 2004
[10] Hardy, G.H., A Mathematician's Apology, Cambridge university Press, 1967
[11] Howe, Roger, et al, Four Reactions to Principles and Standards for School Mathematics, Notices of the AMS, October 2000
[12] May, Kenneth O., Galileo Sequences, a Good Dangling Problem, The American Mathematical Monthly, Volume 79, No. 1, January 1972
[13] Montaigne, Michel de, Of the Education of Children, Montaigne: Selected Essays, Random House, NY, 1940
[14] Plato, Meno, Circa 380 B.C.
[15] Saint-Exupery, Antoine de, Wisdom of the Sands, Amereon Ltd, 2003
[16] Saul, Mark, A community of Scholars: Working
with Students of High Ability in the High School. Developing
Mathematically Promising Students, National Council of Teachers of
Mathematics, 1999
[17] Steinbeck, John, The Grapes of Wrath, Viking Penguin, 1939
[18] Terman, L. M. (1969). The discovery and encouragement of exceptional talent. In D.Wolfle (Ed.), The discovery
of talent (pp. 1–23). Cambridge, MA: Harvard University Press. (Original work published 1954.)
[19] Thurston, William P., Mathematical Education, Notices of the AMS Vol. 37 (1990) 844-850
[20] Winner, Ellen, Gifted Children: Myths and Realities, Reed Business Information, Inc., 1996
George R. Thomas
Executive Director Emeritus
"Nothing can permanently please
which does not contain in itself
the reason why it is so
and not otherwise."
--- Samuel Taylor Coleridge - "Biographia Literaria, Volume I, Chapter XIV"
Page last updated November 18, 2017
Copyright © 2001– MathPath
Send suggestions to webmaster@mathpath.org
|
